INFINI MATHÉMATIQUE

INFINI MATHÉMATIQUE

Le mot «infini» désigne un concept à entrées multiples. Il s’ouvre d’abord sur l’ontologie et signifie alors, selon la tradition, «l’être tel qu’on n’en saurait concevoir de plus grand» («ens quo majus concipi non potest »). Ce fut pour une grande part l’effort de la théologie chrétienne de tenter de montrer, à partir d’un certain moment (saint Anselme), que cet attribut convenait d’une manière adéquate et exclusive au Dieu, objet de la foi, révélé dans l’Écriture. Envisagé de l’autre bord de son champ sémantique, le même mot signifie cependant tout autre chose. On a reconnu très tôt, ainsi qu’en témoignent les fameux arguments de Zénon d’Élée, qu’un segment de droite est divisible «à l’infini». Ici, l’expression «infini» ne désigne nullement un être, mais la simple possibilité de poursuivre un processus opératoire qui, en raison du domaine où il s’effectue et des lois qui le règlent, ne contient en lui-même aucun principe de limitation.

Le concept d’infini mathématique (dont on ne peut pas dire qu’il soit pleinement constitué avant G. Cantor) a été historiquement, et avec des fortunes diverses, élaboré entre ces deux bornes: la borne métaphysique d’une part, qui indiquait la portée maximale du concept; la borne opératoire de l’autre, qui manifestait les contraintes auxquelles se heurtait sa constitution. On pourrait dire que la formation du concept d’infini mathématique a consisté à dégager ces contraintes, à les distinguer, à les classer, et à produire les moyens mathématiquement bien définis de nature à les dominer.

Au cours de ce mouvement, le concept d’infini mathématique a conquis son autonomie: il s’est séparé du concept ontologique, qui s’est alors trouvé renvoyé à un autre champ que celui des mathématiques, bien que sur certains points l’homogénéité du vocabulaire puisse encore prêter à confusion.

À prendre les choses en bloc, on pourra dans cette histoire marquer trois moments. La première phase, purement opératoire, se distingue par trois caractères: l’absence d’un concept positif et pleinement élaboré de l’infini; l’effort pour dégager les difficultés que contient l’usage des processus infinitistes (problème de la divisibilité du continu); l’essai d’élaboration d’une conception de portée limitée, propre à rendre compte des opérations que les mathématiciens pratiquent. En gros, cette phase correspond à l’essor de la mathématique grecque. La problématique philosophique est contenue pour l’essentiel dans la Physique d’Aristote, au livre IV. Elle devait, pour des siècles, dominer les discussions sur l’infini et la divisibilité du continu. Quant aux noyaux opératoires, si l’on met à part les présuppositions techniques de l’argumentation de Zénon, on les retrouvera principalement dans la théorie des proportions due à Eudoxe (livre V des Éléments d’Euclide) et dans les Traités d’Archimède (principalement le Traité de la méthode ).

Dans la deuxième phase, la situation précédente est entièrement renversée. On dispose d’un concept philosophique pleinement élaboré de l’infini. On en trouve chez Spinoza, dans la première partie de L’Éthique , l’expression achevée. Mais, dans le même mouvement, se bouleversent et s’enrichissent les champs opératoires hérités des Grecs. On apprend à dominer les processus infinitistes, dont l’analyse ne relève plus désormais de l’examen dialectique, mais de la mathématique elle-même. L’essor, de Fermat à Leibniz, du calcul infinitésimal va exiger la mise en œuvre d’une nouvelle problématique. Le concept dont on dispose est-il adéquat aux opérations que les mathématiciens pratiquent? Est-il possible de produire un concept de l’infini compatible avec ces opérations et homogène au champ dans lequel elles sont praticables? Leibniz a été ici, comme Aristote en son temps, le penseur qui a délimité pour longtemps les données du problème et dégagé le domaine théorique où l’on pouvait le poser. L’infini mathématique commençait ainsi à gagner le statut d’un concept spécifique dont le contenu exigeait d’être défini à l’intérieur des seules mathématiques.

La phase décisive a été la création cantorienne. Celle-ci s’est produite dans le contexte mathématique propre au dernier tiers du XIX^e siècle. À ce moment, en même temps que s’accomplissait l’arithmétisation de l’analyse, que se dégageaient quelques-unes des structures fondamentales de l’algèbre (groupes et corps), le problème se posait d’étudier le comportement des fonctions les plus générales. La théorie des ensembles de points a été portée au jour comme instrument spécifique de ce renouvellement de la théorie des fonctions. Elle devait profiter de l’algébrisation croissante de tout le corps mathématique. L’analyse de l’infini s’est alors développée en symbiose avec la théorie des ensembles. Elle est devenue entièrement intramathématique. Le cœur de cet édifice, le point de départ d’où a été délimité le champ de problèmes dont certains sont encore aujourd’hui en chantier, a été la conception par Cantor du «transfini». Avec Cantor, le concept d’infini mathématique sort de sa préhistoire.

1. Les Grecs et l’infini mathématique

Les irrationnelles

Nous connaissons par Aristote (Premiers Analytiques , 14, a, 26) en quoi a consisté la rencontre des Grecs avec l’infini mathématique. Ce fut la «découverte», attribuée à un pythagoricien, et qui fit scandale, de l’incommensurabilité de la diagonale du carré. Le premier scolie du livre X des Éléments d’Euclide, en même temps qu’il expose le contenu de la découverte, commente en ces termes la légende selon laquelle celui qui le premier avait divulgué l’irrationalité de 2 aurait péri noyé dans un naufrage: «Les auteurs de la légende ont voulu parler par allégorie. Ils ont voulu dire que tout ce qui est irrationnel et privé de forme doit demeurer caché. Que si quelque âme veut pénétrer dans cette région secrète et la laisser ouverte, alors elle est entraînée dans la mer du devenir et noyée dans l’incessant mouvement de ses courants.» Découvrir 2 c’était entrer dans le lieu où règne la démesure, où s’effacent les contours, où s’accumulent les multiplicités indominables et redoutables, le lieu sans frontières de l’ 見神﨎晴福礼益 (l’indéfini).

Pourtant la «découverte» s’inscrivait rigoureusement dans le champ de la mathématique grecque. Le concept de nombre y comportait deux pôles distincts. Le premier, de nature ontologique, avait été élaboré par les pythagoriciens eux-mêmes: le nombre est pensé comme une essence composée, dont les éléments, essences élémentaires, sont les unités (monades). Ces unités sont pensées comme des points indivisibles. Un nombre est alors une architecture originale construite d’une multiplicité discontinue d’unités-points. Cette conception vivra longtemps dans l’arithmétique des Grecs; on la retrouve au livre VII des Éléments d’Euclide (définitions 1 et 2: «Le nombre est une multiplicité faite d’unités»). Le second pôle est de nature opératoire. Le nombre y est conçu comme lié à l’opération de mesure des grandeurs. Or le nombre-mesure n’est pas exactement le même que le nombre-essence des pythagoriciens. L’unité n’y a pas la même fonction. Elle ne désigne plus (du moins plus nécessairement) l’élément ultime dont le nombre est constitué. Elle désigne simplement un moment dans la chaîne opératoire par laquelle, une grandeur continue (ligne, surface ou solide) étant donnée, on détermine le quantum ( 神礼靖礼益) qui lui convient (longueur, aire, volume): le moment dans lequel on distingue une partie aliquote, choisie arbitrairement, de la grandeur considérée. L’unité n’est plus en ce cas nécessairement posée comme un indivisible.

Dans la «découverte» des irrationnelles, c’est ce second pôle qui a été assumé. Cette effectuation conduisait à chercher à définir le statut des rapports de forme p /q et à les admettre dans le cas, fréquent, où il n’existe pas de nombre entier auquel ce rapport soit égal. Dans le cas du rapport d /c (où d désigne la longueur de la diagonale du carré et c celle de son côté), la fraction d /c n’a pas de statut admissible dans le champ de l’arithmétique pythagoricienne. Son dénominateur c devrait être à la fois pair et impair. Mais, si l’exigence opératoire avait une fois déjà triomphé des contraintes ontologiques, il était cette fois encore prévisible qu’elle en triompherait.

Et, de fait, les «racines irrationnelles» furent admises au nombre des êtres mathématiques. La théorie des proportions, due à Eudoxe, consacre et fonde une telle admission. Nous savons aujourd’hui que ce qui se trouvait construit de la sorte était un système qui, du point de vue opératoire, rendait aux Grecs les mêmes services que nous rend aujourd’hui l’ensemble des nombres réels supérieurs à zéro. Il serait facile de démontrer que la définition, tirée d’Euclide, de l’égalité de deux rapports, est équivalente à la définition, tirée de Dedekind, de l’égalité de deux nombres réels. En construisant la théorie des proportions et celle des racines irrationnelles, les Grecs ont donc bien «rencontré» l’infini mathématique: ils l’ont rencontré sous la forme du continu arithmétique que le concept de rapport permettait d’aborder. Mais qu’ils l’aient rencontré ne signifie pas qu’ils l’aient explicitement reconnu pour ce qu’il était, ni même qu’ils aient dégagé le concept mathématique du continu arithmétique. C’est nous aujourd’hui, nous «post-cantoriens», qui reconnaissons et nommons «infini mathématique» l’objet que, d’une manière oblique, la pratique opératoire des Grecs concernait. Qu’en était-il, sur ce point, des Grecs eux-mêmes? Quels moyens ont-ils mis en œuvre pour tenter de penser ce qu’ils rencontraient?

Zénon

En un premier moment, il semble qu’ils aient pris l’exacte mesure de la difficulté. C’est là une interprétation possible des arguments de Zénon d’Élée, dont Aristote et son commentateur Simplicius nous ont conservé l’essentiel. L’un d’eux (cf. Diels, I, B, 29) est particulièrement instructif pour notre propos. Zénon y expose le «paradoxe» de la grandeur. L’argumentation met en lumière la contradiction entre le pôle ontologique et le pôle opératoire constitutifs du concept de nombre. Si une grandeur doit pouvoir être déterminée par le quantum qui lui convient, comment faut-il la concevoir? Dans l’interprétation pythagoricienne, elle est pensée comme multiplicité d’éléments. Mais, alors, elle ne peut être ni finie ni infinie. La suppose-t-on infinie? Il faudrait la concevoir divisible jusqu’au minimum qui serait nul. Ce minimum ne saurait alors être élément, puisqu’on ne pourrait l’ajouter à lui-même pour produire une grandeur. La suppose-t-on finie? Elle devrait être composée d’éléments indivisibles et séparés. L’intervalle qui les sépare devrait à son tour être un indivisible distinct d’eux. On est ainsi renvoyé au cas de l’infini dont l’examen de la première hypothèse a montré l’impossibilité. La conclusion suggérée est qu’on ne saurait tirer argument de la science du nombre contre l’éléatisme. Le domaine où semble régner le nombre (la grandeur) est étranger à toute multiplicité; les continus linéaires, plans ou solides sont posés comme indivisibles. Pour les mathématiques, la conclusion de l’Éléate constitue une impasse. En liquidant le noyau ontologique hérité des pythagoriciens, il n’a nullement libéré le noyau opératoire: le concept de grandeur lui-même s’abîme dans l’intuition massive du continu parménidien. À travers la conclusion négative apparaît cependant la borne à laquelle se heurtait, sur ce point, l’effort de conceptualisation exigé par la constitution opératoire du «continu arithmétique»: impossibilité de concevoir un infini actuel. Le résultat d’un processus de division poursuivi à l’infini est pensé comme un néant; il n’existe de minimum que nul. L’obstacle était ici la présupposition substantialiste traditionnellement attachée au concept d’élément ( 靖精礼晴﨑﨎晴礼益). Qu’un point soit quelque chose qui n’est rien, voilà qui passait pour impensable. C’était pourtant ce qu’il importait de penser. Faute de pouvoir le penser, il fallut se résoudre à le contourner.

Aristote

De cet effort, né d’une rencontre avec un «objet» dont le statut restait indéterminé, on ne retiendra ici que deux témoignages. Le premier s’inscrit dans le champ de la philosophie: on le trouve pour l’essentiel au livre IV de la Physique d’Aristote. Le second concerne de plus près les techniques mathématiques: il apparaît dans l’œuvre d’Archimède et singulièrement dans cette distance, que le géomètre lui-même a marquée, entre les traités «canoniques» (Traité de la sphère et du cylindre , par exemple) et le Traité de la méthode.

Aristote, on le sait, a nié l’existence de l’infini en acte: il n’existe ni selon l’addition ni selon la division. Le concept d’infini désigne ainsi une simple possibilité idéale. Parler d’un être infini (Dieu ou le monde) est une absurdité: le dernier ciel enveloppe toute chose, à tel point que, selon l’addition, l’infini ne saurait exister, même en puissance. Mais, du même coup, Aristote préserve l’autonomie du champ mathématique, au degré d’abstraction où ce champ se situe. «Ma théorie, écrit-il, n’enlève rien aux considérations des mathématiciens, en supprimant l’infini selon l’accroissement qu’on ne saurait parcourir; car les mathématiciens n’ont pas besoin de l’infini et ne l’utilisent pas: ils ont simplement besoin d’une grandeur finie, choisie aussi grande qu’ils le veulent» (Physique , 207, b, 8). Un texte de la Physique (266, b, 3) nous apprend ce qu’Aristote a dans l’esprit: c’est le fameux «lemme d’Eudoxe» qui sera plus tard énoncé par Euclide (Éléments , X, 1) et qu’Aristote formule en termes assez vagues: «En ajoutant toujours au fini, on dépassera tout fini; en retranchant on tombera au-dessous de tout fini...» Le concept de «grandeur» se trouve alors remanié. Les apories de Zénon sont écartées. Une «grandeur» (i.e. une ligne, une surface, un solide) est pensée comme un continu divisible à l’infini en puissance. Il en va de même du temps, dont Aristote énonce qu’il est «le nombre du mouvement selon l’avant et l’après». Dans cette conception, «points» et «instants» ne sont pas posés comme des constituants, des éléments ultimes dont les continus seraient formés, mais comme des désignations idéales permettant de distinguer sur un continu des intervalles eux-mêmes divisibles à l’infini en puissance. Le «point-élément» des pythagoriciens sort, pour un temps, de l’horizon de la pensée mathématicienne. Le «point» est pensé dans sa fonction: celle d’une frontière idéale. Ces données restent intuitives au sens le plus banal du mot. Les concepts définis sont investis dans un champ, abstrait à partir des données perceptives et dans lequel on se représente les enchaînements d’opérations (dichotomie indéfinie, par exemple) dont ces concepts assurent la régulation. L’arrachement des concepts à ces représentations naïvement intuitives, leur remise en chantier par la racine dans le champ de la pure logique ne seront pleinement effectuables, on le sait, que dans une autre mathésis que celle des Grecs, la mathésis en voie de constitution à la fin du XIX^e siècle, dans laquelle déjà l’analyse était entièrement «arithmétisée».

Archimède

Quant à Archimède, on peut dire que, si d’un point de vue heuristique il a utilisé des méthodes «infinitistes», d’un point de vue théorique (i.e. chaque fois qu’il voulait produire une démonstration canonique) il s’est efforcé de les contourner. Il suffirait pour s’en convaincre de comparer, par exemple, la proposition 1 du Traité de la méthode et les propositions 14, 15, 16, 17 du Traité de la quadrature de la parabole . Le même énoncé y est formulé: l’aire d’un segment de parabole ABC (borné par le segment de droite AC et par la parabole de sommet B) est égale aux 3/4 de l’aire du triangle ABC. Dans les deux traités, le raisonnement met en œuvre des considérations mécaniques telles que des théorèmes établis dans le Traité de l’équilibre des figures planes (cf. en particulier les propositions 14 et 15 du Traité de la quadrature de la parabole ). D’un traité à l’autre, cependant, la différence est grande. Dans le premier cas, l’essentiel de la démarche repose sur un procédé opératoire dont le géomètre se donne la possibilité: décomposer la grandeur dont on cherche à déterminer l’aire en une infinité de tranches, et poser que cette aire doit être la «somme» des aires de ces tranches élémentaires (Archimède énonce: «Considérons toutes les droites parallèles à l’axe qui composent le segment ABC»). Dans le second cas, le cœur du raisonnement consiste à démontrer par la méthode d’exhaustion la proposition 16, ainsi formulée: «Soit Qq la base d’un segment parabolique, la distance de q au sommet de la parabole étant au plus égale à la distance de Q à ce même sommet; soit q E parallèle à l’axe de la parabole et rencontrant en E la tangente à la parabole en Q: l’aire du segment parabolique est égale au tiers de l’aire du triangle Eq Q.» Or, dans la mise en œuvre de la méthode d’exhaustion, Archimède n’opère jamais que dans le fini: il suppose le triangle Eq Q décomposé en tranches égales au moyen des n points de division ¹, ², ..., Oⁿ , marqués sur la base q Q. Il n’est pas question ici de considérer le triangle comme la «somme» d’une infinité de droites. À juste titre, Archimède refuse de donner à la considération d’une telle «somme» un statut mathématique acceptable. Cependant, en dépit de leur distance, il importe de marquer la solidarité des deux démarches. La méthode d’exhaustion permet d’établir en toute rigueur un énoncé dont on dispose déjà. Elle ne permet pas de le découvrir. La «manipulation» des mesures (longueurs, aires, volumes et centres de gravité) dans le champ où elle s’investit (le «continu» objet d’intuition géométrique) semble bien entraîner la mise en œuvre de procès infinitistes, voire la considération, inassimilable en un discours bien formé, d’éléments infinitésimaux (les «droites» du Traité de la méthode ). Cet «envisagement» purement opératoire permet de mettre en lumière des propriétés et des relations cachées. Mais une chose est d’envisager un procès infini, une autre de le penser dans les formes qu’exige la stricte application du principe logique du tiers exclu. Ce qui, à nos yeux encore, fait le mérite d’Archimède, la rigueur de sa démarche proprement démonstrative, marque également la borne qu’il ne saurait transgresser. Rencontré au niveau opératoire l’infini reste privé d’un statut conceptuel qui l’inscrirait dans le champ des objets mathématiques admissibles. Sur ce point, l’activité mathématicienne se meut à la frontière de ce qu’elle peut rigoureusement penser, aveuglée par ses propres normes.

2. L’âge classique

Convenons de nommer «âge classique» la période qui, s’inscrivant dans le champ de la révolution galiléenne, a vu, en même temps que l’essor du cartésianisme et celui des grands systèmes issus de lui, le bouleversement de la cosmologie traditionnelle, l’apparition et l’affermissement du calcul infinitésimal, la mise au jour des principes et des méthodes de la physique mathématique. Cette seule énumération permet de désigner le point où il convient de se placer, si l’on veut, pour l’âge classique, tracer le profil du concept d’infini mathématique. L’œuvre de Leibniz se détache comme la région où se nouent les fils de cet écheveau embrouillé que commence à constituer la question de l’infini.

La rupture du calcul infinitésimal

Marquons d’abord la rupture qu’a été la mise en œuvre du calcul infinitésimal, rupture qui a affecté en premier lieu le niveau opératoire et dont nous pouvons aujourd’hui désigner la racine. Ce fut la triple exigence de définir rigoureusement les concepts cinématiques de vitesse instantanée et d’accélération, de produire les instruments analytiques propres à préciser et à généraliser le concept de courbe, de promouvoir une mathématique qui fût à la hauteur de la tâche théorique inaugurée par Galilée: chercher à exprimer «dans la langue que parle la nature et qui est mathématique» les lois dynamiques qui régissent le mouvement des corps. À l’intérieur du champ mathématique, ces exigences débouchaient sur la mise en évidence de deux concepts: celui de fonction, sans lequel on ne peut donner pleine consistance à l’idée de loi physique; celui de différentielle (ou de «fluxion», dans le langage newtonien), sans lequel il faut renoncer à poursuivre rigoureusement l’analyse locale du mouvement, et donc à en formuler les lois. Cet enrichissement de la mathématique a été pensé comme un retour à Archimède, au-delà de la tradition d’Apollonios (à laquelle, on le sait, Descartes était resté fidèle). Que, dans ce retour, les méthodes archimédiennes aient été déracinées et interprétées, arrachées aux limitations inhérentes à la mathématique grecque, c’est ce dont peuvent nous convaincre bien des déclarations de Leibniz, là où, contre le finitisme cartésien, il en appelle, à son propre avantage et pour marquer la supériorité de son calcul, à l’exemple et à l’autorité d’Archimède. Mais, à s’en tenir là, on ne mesurerait pas toute la force de la rupture. Le développement du nouveau calcul et, après Newton et Leibniz, son rapide essor consacraient un déplacement de la mathématique tout entière. Elle ne s’inscrit plus au ciel éternel où demeurent les essences fixes. Elle se manifeste comme instrument de rationalité, au lieu où est le monde, dans l’organisation des mouvements, dans la contexture des corps, dans l’ordre et la connexion des mesures. Et, si l’établissement de la mathématique en ce lieu exigeait l’usage de dx , il n’y a rien d’étonnant à ce que, en dépit des difficultés logiques auxquelles il donnait lieu, l’infini ait acquis, dans l’analyse en formation, son droit de cité.

Une autre circonstance y a sans doute aidé. Elle ne vient pas de la mathématique, mais de la philosophie et de la cosmologie. En ces domaines, il a fallu affronter l’infini que les Grecs avaient contourné, et s’efforcer d’en constituer un concept. L’élaboration théologique et métaphysique a précédé ici l’exigence cosmologique, qui pour l’essentiel est post-copernicienne (cf. cependant Nicolas de Cues). Mais les deux faces du concept s’articulent sur la même problématique dès l’instant où l’on se pose cette question: «Le prédicat infini convient-il d’une manière univoque à Dieu et au monde?» Question ancienne, mais que le congé donné à la cosmologie du De caelo , le triomphe définitif dans les Principia de Newton des principes galiléens posent désormais en termes neufs. Dans le champ traditionnel, la deuxième partie de la question n’avait de sens qu’ex hypothesi , et pour les besoins de la cause. En admettant qu’il y ait un infini dans les choses, comment le penser, eu égard au seul infini véritable, celui de Dieu? Telle était la forme de la question traditionnelle. Il n’en va plus de même désormais. Si le monde matériel, domaine du mouvement local, est homogène à lui-même en tout point, si les lois qui règnent dans les cieux sont les mêmes que celles de ce monde «sublunaire», alors se trouve posée, pour l’Univers lui-même, la question que posait, dans le champ des grandeurs continues, le problème de leur divisibilité et celui de leur indéfinie extensibilité. La trame de l’Univers n’est-elle pas cet espace homogène dans lequel nous ne pouvons concevoir, ni selon l’addition, ni selon la division aucun principe de limitation? Quelle que soit la réponse que l’on entende ici donner à la question de l’infinité du monde ou à celle de l’infinie divisibilité de la matière, leur mise en œuvre, dans ce champ que la révolution galiléenne a libéré du finitisme aristotélicien, exige l’analyse en une réflexion explicite de la logique interne du concept d’infini. Cette réflexion est à vrai dire un recommencement: la remise en chantier d’un concept que la tradition des théologiens et des philosophes a déjà tourné et retourné en tout sens. Mais cette réflexion n’est plus déracinée: elle s’inscrit au lieu même où s’opère la connaissance effective, au lieu où se constitue l’instrument mathématique propre à la promouvoir. Dès les commencements, nous en trouvons l’indice chez Galilée lui-même. Bien qu’il ait laissé indécise la réponse à la question de l’infinité du monde, il a souligné les exigences appelées par la constitution du concept de l’infini, les contraintes internes auxquelles elles soumettent la pensée: et particulièrement celle-ci, que l’«axiome» qui semble constitutif de la grandeur (le tout est plus grand que la partie) doit y être récusé. Il le montre en construisant entre les entiers successifs et leurs carrés une relation de correspondance univoque et réciproque. Cela, au dire de Pascal, ne devrait pas manquer de donner aux athées un vertige salutaire, mais témoigne d’un renversement remarquable par rapport à la tradition hellénique: mieux valait alors contourner l’infini et sauver la logique; ici, mieux vaut affronter l’infini, quitte à paraître violer les règles d’une logique usuelle.

Ainsi, de trois côtés au moins, l’infini se désigne comme thème d’une réflexion explicite. Établir son statut est, en cet âge classique, une tâche épistémologique fondamentale. Elle s’articule à la fois sur les champs opératoires les plus prégnants (le «calcul») et, à la frontière de la métaphysique et de la cosmologie, sur les domaines spéculatifs les plus anciennement enracinés.

Spinoza

Or cet effort de réflexion se poursuit sur une corde raide. Une distorsion de plus en plus grande se manifeste entre la racine métaphysique du concept et les exigences de thématisation liées à l’usage du calcul infinitésimal, et plus généralement à l’usage d’opérations mathématiquement bien définies. Déjà Spinoza, dans une lettre à Louis Meyer (cf. lettre XII), avait pris soin de distinguer l’«infini véritable», celui de la substance, introduit au début de la première partie de L’Éthique et seul objet d’entendement, du «faux infini», infini selon le nombre, objet d’imagination. À ses yeux, les difficultés dans lesquelles, sur ce point, on s’embarrasse viennent de la confusion entre ces deux infinis. On applique à l’infini productif et indivisible de la substance des modalités opératoires (dénombrement, division, adjonction) qui ne sont praticables et concevables que dans le champ de l’imagination, c’est-à-dire dans un domaine abstrait à partir des données perceptives, domaine où l’on peut désigner des parties, séparer des unités et les composer entre elles selon des règles données. La lettre à Louis Meyer est de 1663: elle précède de deux ans l’établissement du calcul newtonien des fluxions; mais elle est de sept ans postérieure à l’Arithmetica infinitorum de Wallis, qui, transposant dans le champ de l’arithmétique les méthodes de Cavalieri, a sommé des séries infinies convergentes. Aussi, à lire la lettre à Louis Meyer, voit-on apparaître les contraintes que la considération de l’infini dans la pratique des mathématiciens impose au concept de l’«infini véritable». Il est impossible (et Spinoza le marque avec force) de dénaturer la mathématique et de la rejeter tout entière du côté de l’imagination, en déclarant qu’elle n’a jamais affaire qu’au faux infini: elle est, selon Spinoza, science d’entendement en ce que ses définitions, constructives, exhibent l’essence positive du défini. De là l’effort de Spinoza pour tenter de montrer que, dans ce débat, les mathématiciens sont du côté des «vrais philosophes, pourvu qu’ils aient des idées claires et distinctes» (lettre à Simon de Vries): c’est-à-dire pourvu qu’ils ne confondent pas les idées produites dans l’entendement avec les représentations auxiliaires issues de l’imagination (nombre, temps, quantité) qui permettent de poser des opérations et de constituer des calculs. La conclusion à laquelle parvient Spinoza est que «le nombre» (sans doute veut-il dire «l’ensemble des entiers») est absolument inadéquat à l’infini, et qu’on aurait tort de nier l’infini selon l’entendement sous prétexte qu’on ne peut définir de nombre tel qu’on n’en saurait concevoir de plus grand. Mais il faut alors, s’il est vrai que les définitions du mathématicien exhibent l’essence de leur objet, montrer que l’infini de la substance est présent au sein des modes finis sans avoir à se diviser en eux. C’est là la contrainte que l’exigence mathématique fait peser sur le concept ontologique. En posant que cet infini dans le mode est l’essence indivisible du mode fini lui-même, Spinoza donne à entendre que le géomètre récupère cette essence au moment même où, dans son discours propre, il fait usage de cet auxiliaire qu’est le nombre ou, en mécanique, le temps. Une difficulté considérable se lève alors. C’est l’impossibilité où l’on se trouve d’expulser du champ des mathématiques la considération du nombre et le maniement réglé des mesures. À s’y résoudre, on amputerait les mathématiques du concept fondamental qui, depuis Galilée, se constitue: le concept de fonction ; d’autant que, de l’aveu de Spinoza lui-même, le maniement du nombre repose sur des principes qui sont des «vérités éternelles», c’est-à-dire des relations d’entendement. Ce que Spinoza considère comme inadéquation du «nombre» à l’infini (et en cela, comme devait le remarquer Cantor, il a raison) témoigne aussi pour l’inadéquation du concept ontologique (l’infini de la substance) aux exigences et aux contraintes qui se manifestent dans le champ réglé des opérations mathématiques. Ces contraintes portent au premier plan la question du statut des éléments du calcul. Pour les déployer, il ne suffisait plus d’être métaphysicien (ou, comme Spinoza, «géomètre» à l’ancienne mode): il fallait être pris, en algébriste, dans le mouvement de la création mathématique.

Leibniz

Les infinitésimaux

Aux yeux de Leibniz, un calcul est défini par la donnée de ses éléments (les termes du calcul, par exemple les entiers dans l’arithmétique élémentaire) et par celle des lois de composition définies sur l’ensemble de ses éléments: nous dirions aujourd’hui qu’il est défini par le couple (E, face=F0019 行) dans lequel E désigne un ensemble non vide et 行 une classe d’opérations. Dans le cas du calcul infinitésimal, de quoi se compose E? Écrivons, dans la notation usuelle, l’expression:

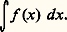Elle comporte une quantité finie f (x ) et une quantité «dx » dont le statut demande à être examiné. Les lois formelles de l’opération notée 咽 exigent que la différence |x 漣 dx | diffère de x «d’aussi peu que l’on voudra». Or, dans le champ des grandeurs usuelles, un calcul n’est effectuable que si les grandeurs considérées sont homogènes. Soit par exemple le matériau mis en œuvre dans la géométrie d’Euclide: points, lignes, surfaces, volumes. Nous disposons ici de quatre ensembles distincts. Si à un ensemble de points distingué sur une droite nous ajoutons des points, nous obtiendrons un nouvel ensemble de points. Pour parler le langage de Leibniz (Die mathematische Schriften , t. V, p. 322), nous augmenterons la «quantité» de l’ensemble initial. Il en ira de même si à un segment de droite nous ajoutons un élément de droite, à une surface un élément de surface, etc. En revanche, nous n’augmenterons pas la quantité initialement donnée si à une ligne nous ajoutons un point, à une surface une ligne, etc. Dans le langage leibnizien, points, lignes, surfaces, volumes sont «incomparables». Selon l’opération nommée «adjonction d’éléments», nous pourrons dire qu’un point est «négligeable» par rapport à une ligne, une ligne «négligeable» par rapport à une surface, etc. Ici se trouve marquée l’entrée du chemin qui, pour un temps au moins, devait, tant bien que mal, donner droit de cité aux «éléments infinitésimaux». Le concept d’«incomparabilité» est sur ce point décisif. Il ouvrait, dès l’origine, la possibilité d’une extension (que Leibniz n’a pas réalisée, et c’est pourquoi la notion d’«élément infinitésimal» reste tellement ambiguë aux commencements du «calcul») qui eût conduit, si elle avait été poursuivie, à construire, comme champ de l’analyse, une extension non archimédienne du système des nombres réels. Ce programme a été réalisé par A. Robinson (Non-Standard Analysis ). Leibniz énonce (op. cit. , t. V, p. 322) qu’on «n’augmente pas la quantité d’une ligne en lui ajoutant une ligne incomparablement plus petite». Par rapport à x , dx «se conduit» comme un point: cela veut dire que dx n’est pas «homogène à x ». C’est-à-dire qu’il n’existe pas d’entier fini n , si grand qu’on le choisisse, tel que ndx 礪 x . D’où la conséquence, extrêmement fâcheuse: ou bien admettre, par coup de force, un nombre infini donné (ce que Leibniz refuse), ou bien construire l’extension non archimédienne permettant de composer, dans le même calcul, les grandeurs finies et leurs éléments infinitésimaux (ce que Leibniz ne pouvait faire). Cependant, comme autrefois, dans l’Antiquité grecque, lors de la «crise» des irrationnelles, l’exigence opératoire a triomphé des réticences liées aux modes usuels de représentation. Leibniz et, à sa suite, G. de L’Hospital ont adjoint au système des grandeurs usuelles (aussi petites ou aussi grandes que l’on veut, certes, mais finies) ces «objets idéaux» que sont les «infiniment petits». Ceux-ci, ainsi que le précise Leibniz, peuvent être pris comme «des notions idéales qui abrègent le raisonnement, semblables à ce qu’on appelle racines imaginaires dans l’analyse commune». Leibniz suggère aussi aux esprits inquiets de ne pas prendre les «infiniment petits» (ou les «infiniment grands») dans «toute la rigueur métaphysique». Cette réticence est instructive: elle indique que Leibniz a bien vu la difficulté, dont la solution eût été d’admettre en mathématiques un infini actuel au sein duquel les éléments «incomparables» eussent trouvé une place canonique. Mais il eût fallu alors construire rigoureusement le concept de ce champ infini. Nous savons aujourd’hui qu’une telle construction exige la mise en œuvre de moyens métamathématiques dont Leibniz ne disposait pas. Il a donc fallu se contenter ici d’un détour rusé: admettre l’«infinitésimale» comme une fiction rationnelle, indispensable à l’art d’inventer, quitte à chercher sa justification dans la métaphysique, dans la monadologie, théorie générale de l’être. La conséquence positive d’une telle admission est la distinction des «ordres de petitesse»: dx «incomparablement petit» par rapport à x , d ²x «incomparablement petit» par rapport à dx , etc.

Le passage à la limite

Conséquence lourde de difficultés: l’exigence de donner un statut au concept de «passage à la limite» et au concept, solidaire, de «quantité évanouissante». Lorsque Leibniz réfléchit au sens de l’écriture:

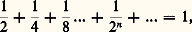pour n croissant indéfiniment, il se demande ce que signifie ici le signe de l’égalité. À rigoureusement parler, ce signe est privé de sens puisque la sommation:

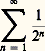ne peut être achevée. Il serait donc absurde de concevoir qu’un segment de droite de mesure 1 est constitué de l’infinité actuelle de ses «parties» de forme 1/2ⁿ . Aujourd’hui, après Cauchy, nous écrivons:

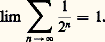Nous pouvons l’écrire en raison de la loi de constitution de la suite (1/2ⁿ ), et parce que nous disposons, sur l’ensemble des nombres réels, d’une définition purement analytique de la convergence. Il n’en allait pas de même aux origines du «calcul» où le concept de série infinie restait encore, à la fois, très opératoire et très intuitif. Aussi Leibniz interprète-t-il le signe de l’égalité en déclarant (op. cit. , t. V, p. 121) qu’aussi loin que l’on poursuive la dichotomie du segment AB de longueur 1 jamais on ne dépassera la borne B (nunquam egredieris terminum B ). Ce qui laisse supposer deux choses: il est toujours possible d’insérer après un terme de la suite un nouveau terme selon la même loi; les différences entre deux termes consécutifs vont décroissant et, au voisinage de la borne B, ces différences se rapprochent de plus en plus de zéro, sans qu’il soit jamais possible de désigner la dernière d’entre elles. L’«égalité» est alors le substitut d’une inégalité, mais d’une inégalité inassignable. L’ambiguïté tient ici à ce que Leibniz manie du même mouvement deux conceptions distinctes: une conception purement ordinale (l’ordre dense de la suite 1/2ⁿ ) et une conception liée à l’intuition du «quantum» (la valeur de la différence entre deux termes consécutifs). Si la première conception pouvait orienter vers la notion de limite, la seconde le conduisit, au voisinage de la borne, à proposer l’idée, à vrai dire métaphysique, de «quantité évanouissante». Seul le principe de continuité (c’est-à-dire ici le principe de l’invariance de la loi de la série en chacun de ses termes) assure l’unité de l’«envisagement» ordinal et de l’intuition «quantitative». Mais alors on accomplit un saut dans le domaine du «comme si». C’est là la vertu du principe leibnizien de continuité (datis ordinatis etiam quaesita sunt ordinata : l’ordre posé dans les données doit s’observer dans leurs conséquences). Ce principe permet de rationaliser l’intuition vague de cette espèce de processus naturel que l’on nomme «passage d’un état à un autre», ou «changement d’état», et dont le mouvement local est la forme la plus simple. Dans l’analyse de ces formes de passage, Leibniz a privilégié les fonctions les mieux connues (celles qui se présentent en cinématique par exemple): les fonctions continues. Il était alors conduit à concevoir le domaine dans lequel ces fonctions sont définies comme un «continu», bien que, sur ce point, il semble n’avoir pas distingué le concept de «continu» du concept de «partout dense». Que l’on considère l’espace (ordre idéal des coexistences possibles), que l’on considère le temps (ordre idéal des successions possibles), que l’on considère l’ensemble organique des êtres réels (la hiérarchie des monades), dans chaque cas le lieu où se repèrent les mouvements, où se définissent les transformations, où agissent les êtres est pensé comme un «continu», une plénitude sans lacunes. Dès lors, pour le concept d’élément infinitésimal, s’opère un glissement du champ de l’arithmétique (ou mieux de l’algèbre), au champ d’une sorte de géométrie abstraite, dont les éléments seraient animés par le dynamisme propre de l’intellect. Pensée comme «incomparable» dans le premier champ, l’infinitésimale est pensée dans le second, c’est-à-dire dans ce domaine de rationalité partout dense (nommé improprement «continu»), comme moment inassignable du passage. L’état de repos sera pris comme état inassignable de mouvement; l’arrêt d’un mouvement à sa borne (par exemple dans l’indéfinie dichotomie du segment AB) comme moment de passage inassignable à la borne, dont on dira qu’elle ne peut être atteinte qu’à la limite. Au cours de ce glissement, qu’autorise la simplification rationnelle constituée par le principe de continuité, tout se passe comme si on avait construit le domaine dans lequel il est permis de composer «grandeurs incomparables» et grandeurs ordinaires. Faute de pouvoir édifier la théorie formelle du système élargi englobant dans le même calcul grandeurs finies et éléments infinitésimaux, on a construit une représentation abstraite, un modèle consistant du domaine dans lequel s’opèrent les passages, se combinent les états, s’édifient les êtres. Dans ce mouvement, le concept de «l’incomparable» est réinvesti, mais dénaturé. Dans le modèle ainsi forgé, les êtres non homogènes sont reliés les uns aux autres par la loi de continuité. Comme le dit Leibniz, ils seront, dans ce domaine, homogônes : la ligne par rapport au point, la surface par rapport à la ligne et, généralement, «l’interminé par rapport au terminé».

Ainsi apparaissent les contraintes inédites que l’essor du «calcul» fait peser sur le concept d’infini mathématique (et, plus généralement, sur le concept d’objet mathématique). D’abord, ainsi que l’a admirablement montré Yvon Belaval (Leibniz critique de Descartes ), c’en est fait, sur ce point, de l’épistémologie cartésienne. On ne peut plus considérer un être mathématique comme formé de la composition de «natures simples» données en une intuition indivisible. En ce «continu» qui constitue le domaine fondamental de rationalité, il n’y a pas de natures simples: tout état distingué en lui y est encore composé à l’infini. Seule la loi (à la rigueur formalisable) de la composition constitue le chemin vers la connaissance. De plus, l’infini mathématique (celui de la série de terme général 1/2ⁿ par exemple) n’est plus un «mauvais infini»: il ne témoigne pas pour la limitation de l’entendement humain qui, incapable d’embrasser l’infini véritable, ne pourrait s’élever au-dessus de la considération de l’indéfini. Cet infini est inscrit dans la nature de l’opération elle-même et en celle du domaine où elle s’effectue. Dieu lui-même ne peut achever la sommation: pour lui comme pour nous l’égalité est ici une «inégalité évanouissante». De là l’exigence d’une remise en chantier des principes de la logique: en particulier, il importe de définir le champ de validité du principe du tiers exclu si l’on veut donner au concept de quantité «évanouissante» le statut de la rationalité. Mais il y a plus. À travers les difficultés que propose un tel concept apparaissent, dans le chantier de l’analyse en voie de constitution, quelques contraintes spécifiques du champ d’objets ici envisagé. La plus fondamentale est celle-ci: comment penser en sa pureté logique la contexture des domaines où sont définies les opérations, construites les fonctions, et pour lesquels sont posés pensables et effectuables les enchaînements propres au calcul infinitésimal? En particulier qu’en est-il du statut de concept de limite? Quelles conditions restrictives concevoir, capables de le fonder rigoureusement? Ces questions, bien qu’elles aient été recouvertes et masquées, jusqu’à l’époque d’A. Cauchy, par l’essor opératoire du calcul lui-même, étaient ouvertes, dès l’origine, dans cette admission, étrange mais nécessaire en son lieu, des éléments «infinitésimaux». Dans la mise en œuvre d’une telle interrogation, le concept d’infini mathématique devait gagner son autonomie et se constituer dans le seul champ de la mathématique. La création cantorienne consacre cette autonomie.

3. Cantor et le «transfini»

Les ensembles infinis de Dedekind

En 1870, Georg Cantor commence sa carrière mathématique en s’attaquant, après B. Riemann et H. Hankel, à l’étude des critères de convergence des séries de Fourier. Depuis longtemps déjà, l’infini mathématique avait cessé d’être une source d’inquiétudes métaphysiques: A. Cauchy, B. Bolzano et K. Weierstrass l’avaient pour ainsi dire réduit à l’état domestique. Le pas décisif avait été accompli ici par Weierstrass. En arithmétisant (pour les besoins de la théorie des fonctions analytiques) le champ de l’analyse, ce dernier avait produit, en dehors de tout appel à l’intuition géométrique, le système d’objets sur lequel pouvaient être définis rigoureusement les concepts de suite infinie, de limite et de convergence: le système des nombres réels. Dans ce système, archimédien, le concept inquiétant de «grandeur infinitésimale» était éliminé. Par là se trouvaient justifiées les précautions formulées jadis par d’Alembert et Lagrange, mais aussi les méthodes pratiquées par Cauchy dans sa recherche de stricts critères de convergence. L’essentiel tenait ici au sens qu’avait pris, dans la pratique mathématique de Weierstrass, l’expression «rigoureusement». Le système avait été produit en une suite d’enchaînements démonstratifs, obtenus par extension et complétion à partir du seul concept de nombre entier et organisés en un système déductif cohérent. Ainsi le prédicat «infini» subissait un nouveau déplacement. Il n’était plus importé dans les mathématiques. Il exigeait au contraire d’être défini dans les formes requises par l’appareil logique mis en œuvre et d’être saisi lui-même comme prédicat spécifique du champ d’objets que l’extension produisait. Sur ce point, un éclaircissement capital devait être apporté par R. Dedekind, lorsque, au début de la décennie 1870, il avait proposé, comme définition des ensembles infinis, la propriété qui, d’après Bolzano, constituait un des paradoxes de l’infini: la possibilité d’établir une correspondance biunivoque entre les éléments d’un ensemble et ceux de l’un de ses vrais sous-ensembles (cf. Richard DEDEKIND). Définition remarquable, car elle éliminait du concept d’infini toutes les considérations confuses concernant les «grandeurs», les «quantités variables», l’«accroissement indéfini». Elle s’articulait fort bien sur les données de l’analyse weierstrassienne. Elle supposait un matériau conceptuel minimal et fort abstrait: la notion (à vrai dire intuitive) d’ensemble («système de choses» disait Dedekind) et celle d’application, que Frege à la même époque définissait en termes purement logiques. Cependant, le concept ainsi posé désignait une pure virtualité. Pour parler le langage traditionnel, l’infini que produit l’application est «syncatégorématique»: il en est de lui comme de l’infini enveloppé dans l’exemple leibnizien de la série:

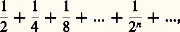qui n’est jamais donnée comme totalité actuelle de ses éléments, mais comme simple possibilité de répéter indéfiniment l’opération qui définit son terme général. Dans le cas de Dedekind, l’«infini» est donné par la médiation de la fonction 﨏 qui détermine la correspondance biunivoque exigée par sa définition. Celle-ci nous permet fort bien d’appliquer le prédicat «infini» à l’ensemble des entiers naturels par exemple. Mais elle ne nous permet nullement de considérer comme bien fondée l’expression «totalité infinie des entiers naturels». Or, s’il est aisé de définir une fonction appliquant d’une manière biunivoque l’ensemble des nombres réels sur l’un de ses vrais sous-ensembles et de désigner cet ensemble comme un «infini syncatégorématique», on est en droit de s’interroger sur la portée du concept ainsi obtenu: Est-il suffisant pour constituer le matériau formel de l’analyse usuelle, épurée par Weierstrass? Est-il même suffisant pour permettre de former le concept de l’application qui le définit? La fonction qu’on attend d’un tel matériau n’exige-t-elle pas que l’ensemble des éléments qui le composent soit pensé comme une totalité donnée actuelle? Dedekind avait été frappé par la difficulté. Il s’était efforcé de produire une sorte de «théorème d’existence» en cherchant à démontrer l’existence d’un «infini donné». Il faisait pour cela appel à la notion, peu claire, de «totalité des pensées». Jadis, Bolzano, dans le même but, avait fait appel à la notion, également confuse, de «totalité des propositions». Mais il est douteux que de telles notions permettent d’aller au-delà de l’infini potentiel, sinon par un coup de force qui pose achevé un système dont on ne dispose qu’en vertu de la loi qui permet d’en désigner les termes. Tel semblait être le prix dont il fallait payer la clarification. À privilégier l’«application» on paraissait se condamner à rester dans le virtuel. Mais alors, qu’en était-il du système des réels? Chassée par une porte (par l’élimination de l’«infiniment petit» et de l’«infiniment grand») la considération de l’infini actuel se présentait à une autre sous la forme d’une question : Quel sens attribuer à la notion de totalité infinie donnée? La notion était-elle destinée à rester vide, simple exigence d’achèvement idéal qu’aucune activité mathématique ne saurait jamais remplir? Pourrait-elle au contraire désigner un jour un être mathématique bien constitué?

Ainsi, à la veille de la création cantorienne, se trouvent marqués, dans le champ de la mathématique, les signes des places vides qu’en son déploiement l’activité mathématicienne doit s’efforcer de combler. Ces signes ne sont pas arbitraires. Ils sont produits à l’intérieur du champ et témoignent de sa structure: complétude des réels, traitement des fonctions discontinues les plus générales, exigence (mise en œuvre par Frege) d’une définition purement logique de l’ensemble des entiers naturels, recherche (inaugurée par Dedekind) d’une méthode d’ordination du continu, autant de questions qui s’articulent sur la donnée préalable d’un concept encore problématique: celui d’ensemble infini, dont il importe de préciser le statut. Le lieu de la problématique exigée n’est plus ici le lieu traditionnel. Il n’est plus question de chercher en un concept ontologique la racine de cet infini «par délégation de pouvoirs» que serait l’infini mathématique. La question est d’une autre espèce: interroger le champ de la mathématique elle-même et chercher en ce champ à produire les systèmes d’énoncés conformes au style de la mathématique, et capables de constituer le concept du domaine de base, hypothétiquement posé comme infini, sur lequel les objets mathématiques sont construits. Une telle démarche est circulaire en ceci que la mathématique est contrainte de reproduire en elle-même l’objet de son propre discours; cependant, en ce dernier tiers du XIX^e siècle, il paraît impossible d’en faire l’économie.

De fait, la difficile mise en œuvre par Cantor, entre 1871 et 1883, du concept de puissance est contemporaine de l’effort de Dedekind, ainsi qu’en témoigne la correspondance entre les deux mathématiciens.

La puissance d’un ensemble

La définition du concept de puissance n’offre pas de difficultés pour qui dispose du concept d’application biunivoque. On dira que deux ensembles (et, à l’origine, Cantor raisonne dans le domaine de l’analyse, c’est-à-dire sur des ensembles de points) ont même puissance s’il est possible de définir, des éléments de l’un vers les éléments de l’autre, une application biunivoque. Le concept de puissance conduit tout naturellement au concept de nombre cardinal, défini comme classe d’équivalence engendrée dans le champ des ensembles de points par l’application biunivoque. Le pas décisif s’accomplit ici dès le moment où Cantor isole la notion du « dénombrable ». Non seulement l’ensemble des entiers est applicable biunivoquement sur l’une de ses vraies parties (sur l’ensemble des nombres pairs, par exemple; il est «infini» au sens de Dedekind), mais on démontre qu’il est équipotent à l’ensemble des couples d’entiers, à l’ensemble des nombres rationnels et à l’ensemble des nombres algébriques. La relation d’équivalence engendre la classe des objets qui sont équivalents selon cette relation; elle donne ainsi naissance à un nouveau concept, celui de «puissance du dénombrable», et au nombre cardinal qui désigne cette puissance, nombre noté par Cantor au moyen de la première lettre de l’alphabet hébreu 尿. De quelle nature est l’objet (face=F0019 尿⁰) ainsi obtenu? L’opération qui permet de l’obtenir n’est pas plus mystérieuse, en son principe, que celle qui nous permettrait d’obtenir, dans le plan, le concept de «direction», par exemple. La seule différence vient ici de ce que la relation d’équivalence a été définie entre des ensembles dont chacun est infini au sens de Dedekind. Aussi est-il impossible de considérer le «nombre» cardinal 尿⁰ comme un nombre fini. Pour exprimer ce caractère non fini, Cantor a inventé un mot: il a appelé 尿⁰ «nombre transfini». Avons-nous ici transgressé l’infini potentiel? On pourrait à la rigueur en douter, si 尿⁰ était seul de son espèce. Mais il n’en est rien, comme le laisse supposer l’indice (0) qui figure dans la notation. L’application du dénombrable sur le continu (l’ensemble des points compris entre 0 et 1 par exemple) nous conduit au-delà du dénombrable. En supposant définie une application biunivoque de N, dénombrable, sur [0,1], Cantor démontre qu’il est possible de définir sur [0,1] un nombre qui n’appartient pas à l’ensemble des images que l’application définit sur [0,1]. Cantor traduit ce résultat en énonçant que la puissance de l’ensemble [0,1] est supérieure à celle du dénombrable. L’itération, sur les continus, de l’application biunivoque permettra de dégager le concept de puissance du continu: l’ensemble [0,1] est équipotent à l’ensemble R des points de la droite réelle, lequel est équipotent à l’ensemble des points d’un carré; plus généralement R est équipotent à Rⁿ . Il y a plus: quel que soit E, de puissance quelconque P, la méthode dite de la diagonale permet de démontrer que l’ensemble des parties de E a une puissance 2^P supérieure à E. Telle est la force de l’application, dont Dedekind faisait la racine de la créativité mathématique: elle ne fournit pas seulement 尿⁰; elle permet aussi de distinguer les puissances et de les nommer en une hiérarchie ordonnée (face=F0019 尿⁰, 2 size=1^尿0, 2² size=1^尿0,...), dont Cantor espère pouvoir démontrer qu’elle constitue un bon ordre. Certes, on le sait, une lacune subsiste: est-on bien en droit d’écrire 尿¹ = 2 size=1^尿0, c’est-à-dire de désigner la puissance du continu comme celle qui, dans la hiérarchie produite, suit immédiatement la puissance du dénombrable? Cantor a répondu par l’affirmation (hypothèse du continu) en raison des conséquences fort utiles qu’une telle hypothèse entraîne en analyse. On sait aussi qu’il espérait, sur ce point, une démonstration, qui, nous en sommes assurés aujourd’hui, ne pouvait être produite; mais, pour notre propos, l’essentiel n’est pas là. Si nous considérons une échelle finie de puissance (par exemple 尿⁰ et 尿¹) il nous est difficile d’écrire 尿¹ 礪 尿⁰ sans considérer l’ensemble représentatif de 尿⁰ comme une totalité achevée, pour laquelle prend tout son sens l’expression «infini actuel». S’il devait en être autrement, on n’échapperait jamais au dénombrable. Il importe cependant de marquer que le concept ainsi proposé (infini actuel) est strictement relatif au champ thématique (le champ des puissances) que procure l’application et n’est pensable qu’en lui. De même que le concept usuel de limite est strictement relatif au champ thématique où il est construit (le corps des réels) et donc ne vaut que pour autant qu’on est capable de produire une théorie correcte de ce champ, de même, ici, il est à prévoir que la validité du concept d’infini actuel va être liée à la possibilité d’établir sur un fondement logique solide la théorie du champ où sont définies les «puissances».

Avec Cantor nous sommes encore loin du compte. La théorie des ensembles abstraits, qu’il propose à partir de 1883 et dont les éléments sont exposés dans deux mémoires publiés en 1895 et en 1897 dans les Mathematische Annalen , reste une théorie naïve. Elle n’est ni axiomatisée, ni, à plus forte raison, formalisée. De plus, contrairement à son contemporain Frege, Cantor a laissé entièrement dans l’ombre la logique sous-jacente. Cependant, il a délimité tout un champ de problèmes dont certains n’ont trouvé que récemment leur solution, il a produit le terrain sur lequel devait se développer la métamathématique contemporaine. En intégrant le transfini dans le corps de l’analyse, du moins sous sa forme ordinale (cf. les problèmes posés par la désignation du dérivé d’ordre 諸, P size=1^諸, d’un ensemble P, défini par:

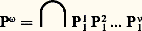quel que soit 益), Cantor a mis en lumière les difficultés sur lesquelles devraient se séparer les écoles de mathématiciens; il a suscité les lieux de rupture: par exemple, le problème d’obtenir une bonne ordination du continu et le problème, connexe, posé par le statut de l’axiome de choix. Il reste que, sur tous ces points, Cantor a, pour ainsi dire, proposé le pari maximal. La question se posera après lui de savoir s’il convenait d’en rabattre ou, au contraire, d’édifier les instruments, logiques et mathématiques, propres à fonder l’admission des êtres qu’il avait définis. Mais désormais cette question, quelle que fût la solution envisagée, ne pourrait se poser qu’à l’intérieur des mathématiques et dans les formes requises par ses exigences de rigueur. L’infini, que des Grecs, à l’origine, avaient côtoyé sans le reconnaître, se trouvait désormais pris dans les mailles du filet mathématique. Comment, sous quelles formes, et avec quelles précautions l’y retenir? Trente ans après les mémoires cantoriens de 1895-1897, en 1925, dans un texte célèbre, David Hilbert devait faire le point des problèmes ainsi posés et proposer les méthodes constructives (substitution, récursion) propres à permettre, par la mise en œuvre de moyens métamathématiques finitistes, la constitution de la «portion» du transfini indispensable à la pratique mathématique. Sur le chemin ouvert par Hilbert, la mathématique d’aujourd’hui est encore engagée. Le concept de l’infini mathématique trouve ainsi, dans la seule mathématique, les principes capables d’assurer sa régulation. Dans un autre champ, le champ ouvert par Cantor, se répète sous une forme spécifique l’effort de thématisation dont Weierstrass avait été, en son temps, l’interprète. Maintenant comme alors, la même question se pose: éliminer du concept d’infini les zones d’ombre que ne manque jamais d’y projeter la représentation spontanée qu’un mathématicien produit du champ où ses propres actes s’enchaînent et se reproduisent.

Encyclopédie Universelle. 2012.